実務で使える静電容量の計算式と具体例！

こんにちは。Noiseです。

Noiseはメーカー勤務でEMCエンジニアとして勤務しています。

今回はiNARTEの試験でも必須科目である静電容量の記事を書いていきます。

静電容量とは、電気的な量を測る際に欠かせない概念です。

静電容量は、電荷が蓄積される能力を表し、コンデンサーや配線、電気機器などの設計や解析において重要な役割を果たします。

本記事では、静電容量の基礎的な概念から、具体的な計算式とその例、応用分野や設計に必要な知識などについて解説します。

また、静電容量がもたらす効果や応用事例についても紹介します。

静電容量について学ぶことで、より正確な電気設計や解析が可能になるだけでなく、高速通信やデータ伝送においても信号の処理や伝送を効率的に行うことができるようになります。

是非本記事を参考に、静電容量についてより深く理解していただければ幸いです。

この記事を読むとわかること。

• 静電容量とは、電荷が蓄積される能力を表す概念であり、電気設計や解析において重要な役割を果たす
• 平行平面コンデンサや同軸円筒、一本線路、平行2線路、球形キャパシタなど、静電容量を計算するための具体的な式と例
• 静電容量の理解により、高速通信やデータ伝送における信号処理や伝送の効率化が可能となる。

最後まで読んでいただけると幸いです。

静電容量とは何か、そして実務での重要性について

静電容量とは、2つの導体間に電位差を加えたとき、その電荷量と電位差の比で定義される値です。

静電容量は、電気回路や電子機器の設計や解析において、信号伝送や電源回路の安定性、ノイズ対策などの面で重要な役割を果たします。

静電容量の計算式の種類と具体例

以下に、代表的な静電容量の計算式と具体例を紹介します。

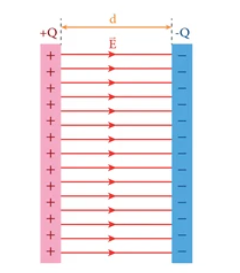
平行平面コンデンサの静電容量

$$ C = \frac{\varepsilon_0\varepsilon_r S}{d} $$

この式では、

静電容量をC

真空の誘電率をε0

誘電体の誘電率をεｒ

導体の面積をS

導体の間隔をdとしています。

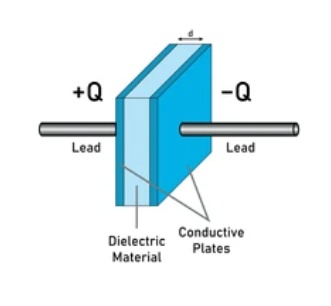
平行平面コンデンサとは、2枚の平面の導体を平行に配置し、その間に誘電体を挟んだもので、電気的なエネルギーを蓄える装置です。

この式を使うことで、平行平面コンデンサの静電容量を計算することができます。

具体例

平行板の面積が10cm×10cmで、板間距離が1mmの平行板コンデンサの静電容量を求める。

$$
C = \frac{(8.85 \times 10^{-12} \times 1 \times 0.01)}{1 \times 10^{-3}} = 8.85 \times 10^{-11} \text{F}
$$

同軸円筒の静電容量

この式は同軸円筒の静電容量を求める式です。

同軸円筒は、中心に導体があってその周りにもう1つの導体がある構造を持っています。

この構造は、高周波信号を送受信する際に一般的に用いられます。

$$ C = \frac{2\pi\varepsilon_0\varepsilon_r L}{\ln(b/a)} $$

ここで、Cは同軸円筒の静電容量を表しています。

ε₀は真空の誘電率

ε_rは誘電体の誘電率

Lは同軸の長さ

bは外側の導体の半径

aは内側の導体の半径を表します。

また、LNは自然対数を表す関数です。

大地上の一本線路の静電容量

大地上の一本線路の静電容量を求める式は、以下の通りです。

$$ C = \frac{2\pi\varepsilon_0\varepsilon_r}{\cosh^{-1}(h/a)} $$

この式では、

静電容量をC

真空の誘電率をε₀

誘電体の誘電率をε_r

導体間の距離をh

導体の半径をa

としています。

具体例

高さが10m、半径が1cmの一本線路の静電容量を求める。

C=2π×8.85×10^-12×1×10^-2/cosh^-1(10/0.01)=18.8 pF

平行2線路（線間が小さい場合）の静電容量

長さdの平行2線路の静電容量を表す式は次のようになります。

$$ C = \frac{d \cdot \pi \varepsilon_0}{\cosh^{-1}(R/2a)} $$

• C：静電容量（ファラド）
• d：線路の長さ（メートル）
• R：2本の線路の半径（メートル）
• a：線路の間隔（メートル）
• ε₀：真空の誘電率（8.85×10^-12 F/m）

具体例

線間が1cm、半径が0.5cmの平行2線路の静電容量を求める。

C=1×π×8.85×10^-12/cosh^-1(0.5/0.01)=94.1 pF

平行2線路（線間が大きい場合）の静電容量

長さがdで、線間距離がRである平行2線路の静電容量Cは、

$$ C = \frac{d \cdot \pi \varepsilon_0}{\ln(R/a)} $$

と表されます。ここで、ε0は真空の誘電率であり、aは線路の半径を表します。

具体例

線間が10cm、半径が1cmの平行2線路の静電容量を求める。

C=1×π×8.85×10^-12/LN(1/0.1)=1.26 pF

球形キャパシタの静電容量

球形キャパシタの静電容量を求める式は以下の通りです。

 $$ C = \frac{4\pi\varepsilon_0\varepsilon_r ab}{b-a} $$

ここで、静電容量をC、真空の誘電率をε0、誘電体の誘電率をεr、内半径をa、外半径をbとしています。

具体例

内半径が1cm、外半径が2cmの球形キャパシタの静電容量を求める。

C=4π×8.85×10^-12×1×10^-2×(2×10^-2×1×10^-2)/(2×10^-2-1×10^-2)=3.51 pF

静電容量のエネルギーについて

静電容量を持つコンデンサに電荷を蓄えると、電場が生じます。

この電場によって、コンデンサに蓄えられた電荷を別の回路に放出することができます。

このとき、コンデンサに蓄えられたエネルギーは以下の式で表されます。

$$ W = \frac{1}{2}CV^2 $$

ここで、

Wはコンデンサに蓄えられたエネルギー（ジュール）、

Cは静電容量（ファラド）、

Vはコンデンサにかかる電圧（ボルト）です。

実務での静電容量の応用事例について

静電容量は、電気回路や電子機器の設計や解析において、様々な応用があります。

例えば、以下のようなものがあります。

• 信号伝送回路における信号品質の向上
• 電源回路の安定化
• 高周波回路におけるインピーダンスマッチングのための回路設計
• 電気容量の大きいコンデンサを使ったノイズフィルタリング
• 電気静力学的問題の解析や設計（例えば、電気感受性を持つセンサの設計など）
• 電界制御を利用した粒子分離や精製プロセスの開発

静電容量は、その性質上、高周波信号や高速信号の伝送や処理にも関係しています。

例えば、高速通信やデータ伝送においては、信号の増幅や波形整形のために、高速スイッチング回路やディジタル信号処理回路において、静電容量を考慮した設計が必要です。

また、電力系統の設計や解析においては、配電線路や変圧器などの電力機器の静電容量を正確に評価することが必要です。

静電容量が大きい機器においては、高電圧が印加された際の放電現象などの影響も考慮する必要があります。

まとめ

本記事では、静電容量の基礎的な概念や具体的な計算式と例、応用分野や設計に必要な知識などについて解説しました。

静電容量は、電気設計や解析において不可欠な概念であり、高速通信やデータ伝送においても重要な役割を果たしています。

静電容量の理解により、正確な設計や解析が可能となるだけでなく、信号処理や伝送の効率化にもつながるため、今後ますます重要性が高まっていくと考えられます。

またiNARTEの試験でも静電容量を用いた問題はとても多く出題されるので、しっかりと身につけましょう！

以上です。

面白かった、ためになったという方は、下記をクリックしていただけると励みになりますので、よろしくお願いいたします！

おすすめの書籍

【スポンサーリンク】