
こんにちは。Noiseです。
Noiseはメーカー勤務でEMCエンジニアとして勤務しています。
今回は、電磁気学の分野でよく使われるLC共振回路の共振周波数の求め方について解説します。
LC共振回路は、信号のフィルタリングやノイズの除去などに広く利用されており、回路設計やテストにおいて重要な役割を果たしています。
特に、共振周波数は回路の特性を決定する重要な要素の一つであり、その計算方法を理解することが設計やテストを行う上で必要不可欠です。
そこで、この記事ではLC共振回路の共振周波数について、計算方法の解説と実務での活用方法について説明します。
LC共振の周波数計算は、一番実務で使用する計算式になりますね!
この記事を読むとわかること。
- LC共振回路の共振周波数の計算方法とその重要性について理解できる。
- LC共振回路が信号のフィルタリングやノイズ除去などに広く利用されていることがわかる。
- 実際の回路設計やテストにおいて、共振周波数の計算が重要な役割を果たしていることがわかる。
最後まで読んでいただけますと幸いです。
LC共振回路とは?
LC共振回路とは、コイル(inductor)とコンデンサ(capacitor)を組み合わせた回路のことです。
この回路は、共振周波数の周波数帯域で電気信号を通過やカットすることができます。
一般に、EMC(電磁環境適合性)に関連する回路設計やテストにおいて、LC共振回路は非常に重要な役割を果たします。
↓回路図でいうとこんな回路ですね↓
LC共振回路の共振周波数とは?
LC共振回路の共振周波数とは、回路内のコイルとコンデンサの特性によって決まる周波数のことです。
この周波数では、コイルとコンデンサの両方が同時に最大のエネルギーを持ち、回路内の電圧や電流が最大になります。
下記は1uHのコイルと1uFのコンデンサを並列で回路に接続した例になります。
横軸が周波数、縦軸がインピーダンスになりますが、159kHzでインピーダンスが最大となっていることがわかります!
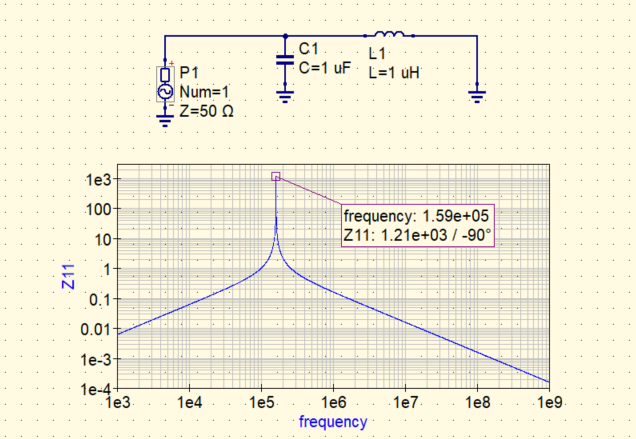
インピーダンスが最大ってことは急激に電流が流れなくなっているということですね!
また上記のような共振周波数の解析は下記記事のQucsを用いて可能です。
共振周波数の計算方法
共振周波数は、以下の式で計算することができます。
f=1/2π√LC
ここで、
fは共振周波数(単位はHz)
Lはコイルのインダクタンス(単位はHenry)
です。
実際の計算例
先ほどのこちらの回路で計算してみましょう!

コイルのインダクタンスが1μH
f=1/2π√LC
f=1/2π√(1×10^-6)(1×10^-6)
f=1/2π√1×10^-12
f=1/2π×1×10^-6
f=159.1kHz
シミュレーション通りの結果になりましたね!
実務での使い方
LC共振回路の共振周波数は、回路の設計やテストにおいて非常に重要な役割を果たします。
回路の共振周波数を正確に計算することで、回路の動作を最適化することができますね。
また、LC共振回路を使用して、信号のフィルタリングやノイズの除去などの目的で、周波数帯域で信号を通過や減衰させることができます。
今回の回路の例では159kHzピンポイントで信号を減衰させるフィルタになりましたね!
これはいわゆるノッチフィルターというものになりますね。
まとめ
LC共振回路の共振周波数は、回路内のコイルとコンデンサの特性によって決まる周波数であり、共振周波数を正確に計算することが回路設計やテストにおいて非常に重要ということがわかりました。
共振周波数は、f=1/2π√LCの式で計算することができます。
とっても簡単な公式ですね!
LC共振回路を使用すれば、信号のフィルタリングやノイズの除去などの目的で周波数帯域で信号を通過、減衰させることができますね。
また回路設計やテストにおいて、LC共振回路は非常に重要な役割を果たします。
共振周波数の計算方法を理解し、実務での使い方を熟知することで、回路の設計やテストを効率的に行うことができます。
共振周波数の計算はiNARTEのテストにも出題されるのでしっかり覚えましょう!!
最後に例題
例題:
コイルのインダクタンスが50μH、コンデンサのキャパシタンスが0.1μFの場合、LC共振回路の共振周波数を計算してください。
解答:
f=1/2π√LC
f=1/2π√(50×10^-6)(0.1×10^-6)
f=1/2π√5×10^-12
f=1/2π×2.236×10^-6
f=1.591kHz
この例題の場合、LC共振回路の共振周波数は1.591kHzとなります。
おすすめ書籍
以上です。
面白かった、ためになったという方は、下記をクリックしていただけると励みになりますので、よろしくお願いいたします!
【スポンサーリンク】
【スポンサーリンク】